Construcción de G
El Problema del Árbol Capacitado (CTP - por sus siglas en ingles) es definido de la siguiente manera:
Dada una matriz de n*n de distancias enteras y dos enteros c y K, Existe un árbol de expansión mínima de n nodos con costo total K o menor, tal que al remover el nodo 1 resulte en componentes conectados de cardinalidad que no excede c?
Theorem 1 El CTP es NP Completo
Proof. Primeramente se observa que el CTP es NP, dado que mediante un algoritmo no determinista, podemos adivinar uno por uno los arcos del árbol, entonces verificar que las condiciones de la definición del árbol del CTP se mantienen.
Ahora procedemos a mostrar una transformación del problema de SAT al CTP. Sea B una instancia de SAT con variables X1...Xn y claúsulas C1,...,Cm.
Se construirá una instancia G de CTP con 2n+2m+1 nodos, capacidad c = n+m, y costo K = 2n+3m tal que dicha instancia tiene una solución válida con costo K o menor si solo si B es satisfactible.
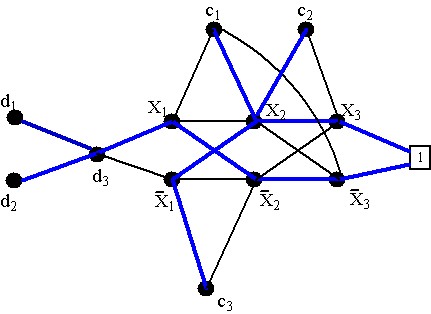
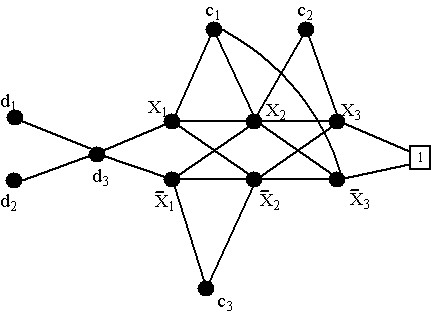
Para cada variable Xi de B, G tiene dos nodos Xi y [`(Xi)] ; existen arcos de costo 1 entre los nodos Xi, [`(Xi)] y los nodos Xi+1,[`X]i+1 para i = 1,2,...,n-1. También existen arcos de costo 1 entre el nodo concentrador y X1, [`X]1. Para cada claúsula Cj de B existen dos nodos cj y dj en G. Los nodos d2,...,dn son ligados a d1 con un arco de longitud 1, y d1 es ligado a Xn, [`X]n, nuevamente por un arco de longitud 1. Finalmente, unimos cj y Xi(o [`X]m) con un arco de longitud 2 si la literal Xi(o [`X]i) esta en la claúsula Cj, todas las otras distancias son puestas a infinito. Con esto queda completa la construcción de G.
Ahora se probará que B es satisfactible si y solo si G tiene un árbol capacitado T con costo K o menor.
Supóngase que tal árbol T existe, primero observese que T debe tener 2n+2m arcos (dado que tiene 2n+2m+1 nodos). Dado que los nodos c1,...,cm son incidentes sobre los arcos de costo 2 o mayor, al menos m arcos en T tienen costo 2. Dado que K = 2n+3m, y que el arco más corto de G tiene longitud 1, entonces T consiste de estos m arcos de longitud 2, y 2n+m arcos de longitud 1. Además, dado que existen dos arcos de longitud 1 incidentes sobre el nodo 1 y c es la mitad del número de terminales en G, T tiene exactamente dos ramas, cada una de cardinalidad n+m. Los m nodos d1,...,dm están en una de estas ramas. La única forma en que estos nodos pueden ser conectados a 1 (dado que c1,...,cn deben ser hojas de T) es mediante una trayectoria P recorriendo un nodo por cada par {Xi, [`(Xi)] }.
Piénsese en el hecho de que un nodo esta en P significa que la literal correspondiente tiene valor FALSO. Dado que los nodos d1,...,dm junto con P agotan los m+n vértices permitidos en una rama, los nodos restantes {Xi, [`(Xi)] } y {cj} deben constituir la otra rama.
Consecuentemente, para cada cj,hay un nodo que no esta en P, tal que cj es conexo a este. Por lo tanto cada claúsula de B contiene una literal a la cual le es asignada el valor de verdadero, por la asignación de verdad anterior.
Asi B es satisfactible.
Reciprocamente, asúmase que existe una asignación de verdad t satisfaciendo B. Es relativamente sencillo observar que, invirtiendo los argumentos anteriores se puede encontrar un árbol t valido con costo K.
Con esto el teorema queda demostrado.
Example 2 Sea B = ([`X]1+X2+X3)(X1+X2)([`X]2+[`X]3) una fórmula y X1 = X2 = V, X3 = F. En la siguiente figura se muestra el grafo G correspondiente.